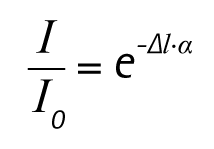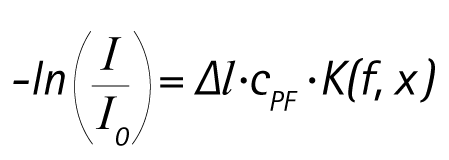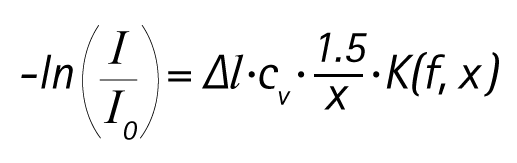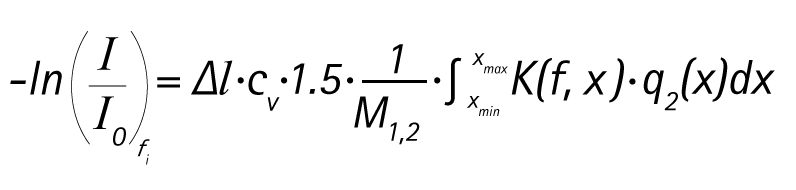Particle size and concentration analysis with ultrasonic extinction
Ultrasound analysis technology is highly multifaceted. Distance, speed, through-flow, boundary layers and many other parameters can be measured in a non-destructive way using ultrasound. Particle size distributions can also be determined from how particles interact with ultrasonic waves. To achieve this, the particles must be in a fluid medium in which the ultrasound can spread out, meaning that ultrasonic extinction can be used for the analysis of suspensions and emulsions.
The differences between laser-optical and acoustic ultrasound methods are less significant than one might think. In both cases, waves interact with particles, and the defining parameter is the size ratio of wave to particle.
However, in contrast to optical methods, the intensity of a sonic wave can be determined over many frequency decades with just one receiver. At the same time, the reception properties of ultrasound receivers are far more direction-dependent than with light detectors. They are highly insensitive to signals that do not hit the receiver surface at a precise right angle. As repeated diffusion and diffraction of the ultrasonic signal to different particles (multiple scattering) contributes to signal deflection, the reception of these unwanted signal components is inherently eliminated. This simplifies theoretical description of the measuring signals, making this method particularly well-suited for use with high product concentrations. The world of ultrasonic extinction begins at the point where light no longer penetrates the sample material as a result of high particle or droplet density. Highly concentrated mineral slurries, deep-black crude oil suspensions, viscous pastes and crystal mushes are all standard applications for ultrasonic spectroscopy.
Ultrasound principle
Particles and droplets embedded in a liquid matrix are acoustically detected from the exterior via impulse. Low-energy ultrasound is passed through an opaque suspension or emulsion layer. For this purpose, an ultrasonic transmitter and receiver stand opposite one another, plane-parallel, at a distance of a few millimetres. The suspension or emulsion to be analysed is passed between them. The sonic waves that reach the receiver side are recorded and evaluated. If the sonic waves spread through the pure liquid practically without hindrance, then these are scattered and reflected if disperse phases are present.
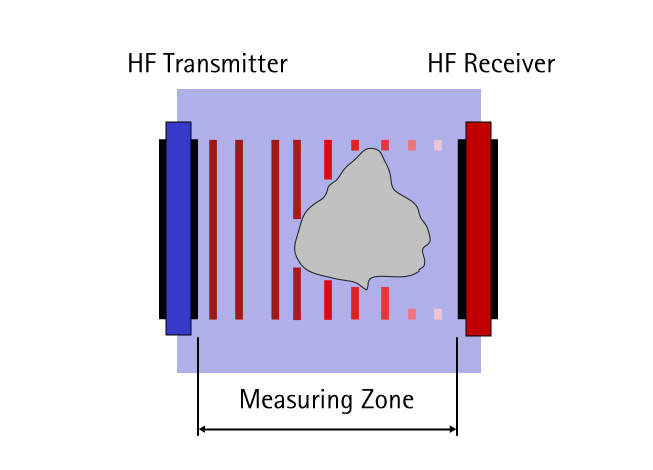
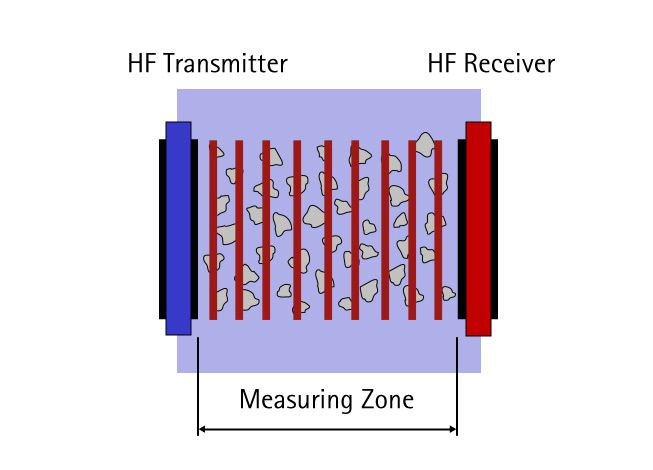
Deflection of waves from their direction of origin leads to loss of acoustic energy on the receiver side. This effect – also referred to as acoustic damping – is determined by the size ratio of wave to particle. Comparatively small particles exert little damping effect on sonic waves. The measuring effect increases as particle size rises. If both large and small particles are present at the same time, strong and weak damping effects will overlap.
As with optical waves, the Beer-Lambert law applies to the physical description of the acoustic effect. This takes a simple form if monodisperse particle sizes are assumed.
The equation shows a logarithmic correlation between the measuring effect on the left and, on the right, the thickness of suspension layer Δl, solid volume concentrationcvol , and a reciprocal correlation with particle size x. The -ln(I/I0) measurement is referred to as acoustic damping or sonic extinction. The K(f,x) factor is the extinction cross-section and describes the interaction of particles in a suspension with the ultrasonic waves, depending on size ratio and the interacting materials.
The same number of damping measurements with different frequencies are required in order to include multiple particle size classes. The resulting damping spectrum is calculated by software on the basis of the underlying individual spectra (ideal damping spectra) and their proportional share in the overall spectrum. These shares represent the particle size distribution.
As the sum of all particle fractions included is standardised to 100%, this condition presents a further equation, which enables the constant cV – i.e. the volume concentration of the disperse phase – to be calculated.
Evaluation and evaluation modes
The spectra described above as “ideal damping spectra” are assumed to be known in the evaluation for each particle size class. This theoretical correlation between measured damping effect and causative particle size is described via the extinction function K(σ). The ratio of particle size and wavelength is amalgamated in the dimensionless parameter σ. The extinction function summaries the dependence of the extinction cross-sections K(f,x) in a curve. This offers various opportunities to make the material-dependent extinction function accessible.
The product-specific extinction function can basically be theoretically calculated from a range of substance data, such as density, viscosity, and sound velocity. However, this presupposes a few idealised assumptions, for example entirely round particles with smooth, unbroken surfaces, isotropic properties, pure and simple material systems, and many more. Although solid systems of this type are almost never encountered in practice, simple 2-phase systems can in fact be found when it comes to emulsions. For these systems, the theoretical correlation between frequency-dependent damping and droplet size can be very successfully calculated from the substance properties of sound velocity, density and viscosity, and the absorption coefficient of the liquid phases concerned. The absorption coefficients of the two phases can be calculated with the ultrasound spectrometer itself.
Most real-life material systems do not contain any perfectly round particles with unbroken surfaces, and the particles are only rarely isotropic or pure substances. However, in order to maintain the extinction function, material systems such as these – most of which are suspensions – are made accessible through empirical comparison. An ultrasonic extinction measurement is carried out on a sample of the suspension to be investigated. The extinction function can only be calculated from the above equation if the particle size distribution, the concentration and the breadth of the measuring gap used Δl are known. While the concentration of the sample can usually be determined easily, particle size distribution can only be identified using a comparative measurement, for example by sifting or laser diffraction. The extinction function for the material system under investigation can then be calculated using software tools. Once determined in this way, the function then continues to be available for evaluating extinction analyses, and does not need to be redetermined. In practice, having a broad selection of extinction functions reached in this way often makes it unnecessary to redetermine this parameter.
The particle-wave interactions described so far are less relevant for dispersions with submicron-sized particles (small particles with relatively large sonic waves). Instead, the largest share of sonic energy is produced via viscous and friction losses between the particles themselves and with the dispersion medium. The relevant parameters for describing this effect are the densities of the phases and the viscosity of the liquid. The particle size distribution can be calculated directly if these parameters are known.
In practice, it is apparent that the majority of all products in the micrometre and millimetre range can be described very well using just a small selection of extinction functions. Variations in physical and chemical properties between products are often negligible. So, for example, very different minerals can always be evaluated using the same function, without having to accept any noticeable losses of quality in particle size analysis. The same applies for crystalline products or plastics. As a result, ultrasonic extinction is practical and reliable to use, and has become established in industrial and scientific use. We make the use of ultrasonic extinction possible for a wide range of applications with the OPUS process measuring system and NIMBUS desktop device